Quickstart#
In this quickstart example, we’ll fit scDiffEq to the LARRY in vitro hematopoietic differentiation dataset, which uses lineage tracing to track cell fate decisions during differentiation. After fitting a model, we’ll visualize the inferred dynamics and generatively simulated developmental trajectories from the model. Finally, we’ll project our predicted trajectories back into the original gene space. The LARRY dataset provides scRNA measurements at multiple time points, enabling us to study
the temporal dynamics of hematopoietic differentiation. Here, we’ll look at granular (dt=0.1d) changes in gene expression over real time.
A note on hardware#
Here, we’re using an NVIDIA T4 GPU (available for free in Colab). However, this package runs well on Apple Silicon (tested on M1) and cpu. Thanks to the LightningAI framework on which scDiffeq was built, you don’t have to make any adjustments when switching hardware; it will automatically be recongized.
[1]:
import scdiffeq as sdq
print(sdq.__version__, sdq.__path__)
1.0.0rc0 ['/Users/mvinyard/GitHub/scDiffEq/src/scdiffeq']
Load data#
Here we’ll use the LARRY (Lineage tracing on transcriptional landscapes links state to fate during differentiation) in vitro dataset, which combines single-cell RNA sequencing with lineage tracing to study hematopoietic differentiation.
Dataset: The LARRY dataset provides comprehensive lineage tracing data for studying cell fate decisions during in vitro hematopoietic differentiation.
[2]:
adata_ref = sdq.datasets.larry(data_dir="/Users/mvinyard/data/")
adata_ref
scDiffEq [INFO]: Loading data from /Users/mvinyard/data/scdiffeq_data/larry/larry.h5ad
[2]:
AnnData object with n_obs × n_vars = 130887 × 2492
obs: 'Library', 'Cell barcode', 'Time point', 'Starting population', 'Cell type annotation', 'Well', 'SPRING-x', 'SPRING-y', 'clone_idx', 'fate_observed', 't0_fated', 'train', 'ct_score', 'ct_pseudotime', 'ct_num_exp_genes'
var: 'gene_ids', 'hv_gene', 'must_include', 'exclude', 'use_genes', 'ct_gene_corr', 'ct_correlates'
uns: 'fate_counts', 'h5ad_path', 'time_occupance'
obsm: 'X_clone', 'X_pca', 'X_scaled', 'X_umap', 'cell_fate_df'
layers: 'X_scaled'
Preprocessing#
[3]:
import umap
UMAP = umap.UMAP(n_components=2)
adata_ref.obsm["X_umap"] = UMAP.fit_transform(adata_ref.obsm["X_pca"])
Subset for example
[4]:
nm_clones = adata_ref.uns["fate_counts"][["Monocyte", "Neutrophil"]].dropna().index
adata_ref.obs['nm_clones'] = adata_ref.obs["clone_idx"].isin(nm_clones)
MASK = adata_ref.obs["Cell type annotation"].isin(["Monocyte", "Neutrophil", "Undifferentiated"]) & adata_ref.obs['nm_clones']
adata = adata_ref[MASK].copy()
del adata.obsm['X_clone']
del adata.obsm["cell_fate_df"]
adata.obs.index = adata.obs.reset_index(drop=True).index.astype(str)
Define the model#
Here we’ll define the model with sdq.scDiffEq - the container class for the algorithm and learned model. Under the hood, the sdq.scDiffEq uses three key components:
Components of the sdq.scDiffEq model#
The
LightningDataModule. The formatted dataThe
LightningDiffEq. The neural differential equation implemented for our specific use-case. There are several of these.The
Trainer.
Together, these three objects complete the basic circuit of a PyTorch Lightning model training workflow.
The sdq.scDiffEq is very customizable. The LightningDiffEq is the workhorse for our key contributions; there are several LightningDiffEq backends that may be called - each using different assumptions - and it is further customizable. By defualt we’ll fit a drift-diffusion SDE composed of two PyTorch neural networks (torch.nn.Module). The drift network will consist of two hidden layers of 512 nodes while the diffusion network will be two layers of 32 nodes. The input to each
network will be a given cell state. By default this cell state is selecetd as adata.obsm['X_pca'].
A note on time#
A required input to sdq.scDiffEq is time, communicated using a column in adata.obs. This dataset provides time as adata.obs['t'], which sdq.scDiffEq automatically recongizes.
[5]:
model = sdq.scDiffEq(adata)
scDiffEq [INFO]: Input data configured.
Velocity Ratio params [configure_model]: {'target': 2.5, 'enforce': 100, 'method': 'square'}
Seed set to 0
Fit the model#
Now that the model is defined, we are ready to fit the model to the given data. The model will automatically log training progress to an adjacent directory. This dataset and training configuration will only use <1 Gb of memory on our T4 GPU.
[6]:
model.fit(train_epochs=1500)
scDiffEq [INFO]: Detected environment: jupyter
GPU available: True (mps), used: True
TPU available: False, using: 0 TPU cores
| Name | Type | Params | Mode | FLOPs
---------------------------------------------------------------------------
0 | DiffEq | PotentialSDE | 293 K | train | 0
1 | sinkhorn_divergence | SinkhornDivergence | 0 | train | 0
---------------------------------------------------------------------------
293 K Trainable params
0 Non-trainable params
293 K Total params
1.174 Total estimated model params size (MB)
24 Modules in train mode
0 Modules in eval mode
0 Total Flops
[09:15:22] Epoch 10/1500 | (3.72s) | train loss: 252.68, val loss: 269.71
[09:16:01] Epoch 20/1500 | (3.85s) | train loss: 391.40, val loss: 391.82
[09:16:43] Epoch 30/1500 | (3.66s) | train loss: 430.47, val loss: 438.60
[09:17:22] Epoch 40/1500 | (3.83s) | train loss: 377.66, val loss: 384.02
[09:18:05] Epoch 50/1500 | (4.98s) | train loss: 306.82, val loss: 294.70
[09:18:49] Epoch 60/1500 | (4.13s) | train loss: 246.34, val loss: 239.51
[09:19:32] Epoch 70/1500 | (4.24s) | train loss: 212.55, val loss: 216.34
[09:20:13] Epoch 80/1500 | (3.78s) | train loss: 179.02, val loss: 173.92
[09:20:53] Epoch 90/1500 | (3.74s) | train loss: 162.29, val loss: 207.44
[09:21:34] Epoch 100/1500 | (3.80s) | train loss: 145.43, val loss: 280.11
[09:22:13] Epoch 110/1500 | (3.78s) | train loss: 137.01, val loss: 135.45
[09:22:53] Epoch 120/1500 | (3.73s) | train loss: 120.60, val loss: 138.62
[09:23:36] Epoch 130/1500 | (3.83s) | train loss: 115.02, val loss: 124.18
[09:24:16] Epoch 140/1500 | (3.81s) | train loss: 122.11, val loss: 116.36
[09:24:56] Epoch 150/1500 | (4.01s) | train loss: 109.85, val loss: 114.50
[09:25:36] Epoch 160/1500 | (4.25s) | train loss: 107.38, val loss: 150.19
[09:26:16] Epoch 170/1500 | (4.17s) | train loss: 100.09, val loss: 201.71
[09:26:56] Epoch 180/1500 | (3.80s) | train loss: 99.88, val loss: 131.98
[09:27:41] Epoch 190/1500 | (4.57s) | train loss: 92.36, val loss: 133.30
[09:28:29] Epoch 200/1500 | (5.51s) | train loss: 101.12, val loss: 104.71
[09:29:15] Epoch 210/1500 | (4.27s) | train loss: 92.34, val loss: 117.17
[09:30:00] Epoch 220/1500 | (4.45s) | train loss: 92.58, val loss: 90.20
[09:30:49] Epoch 230/1500 | (4.60s) | train loss: 90.71, val loss: 98.94
[09:31:36] Epoch 240/1500 | (3.92s) | train loss: 94.48, val loss: 106.39
[09:32:22] Epoch 250/1500 | (4.67s) | train loss: 95.52, val loss: 120.43
[09:33:09] Epoch 260/1500 | (4.63s) | train loss: 87.05, val loss: 107.74
[09:33:57] Epoch 270/1500 | (3.78s) | train loss: 90.34, val loss: 103.32
[09:34:37] Epoch 280/1500 | (4.01s) | train loss: 100.29, val loss: 117.22
[09:35:18] Epoch 290/1500 | (4.33s) | train loss: 99.75, val loss: 173.45
[09:35:59] Epoch 300/1500 | (3.75s) | train loss: 84.21, val loss: 116.03
[09:36:38] Epoch 310/1500 | (3.70s) | train loss: 85.80, val loss: 113.28
[09:37:17] Epoch 320/1500 | (4.11s) | train loss: 86.42, val loss: 165.78
[09:37:56] Epoch 330/1500 | (3.65s) | train loss: 86.87, val loss: 109.63
[09:38:35] Epoch 340/1500 | (3.84s) | train loss: 95.25, val loss: 120.41
[09:39:14] Epoch 350/1500 | (3.80s) | train loss: 89.23, val loss: 120.61
[09:39:53] Epoch 360/1500 | (3.72s) | train loss: 90.54, val loss: 123.41
[09:40:32] Epoch 370/1500 | (3.80s) | train loss: 87.33, val loss: 113.61
[09:41:17] Epoch 380/1500 | (4.06s) | train loss: 89.90, val loss: 100.88
[09:42:01] Epoch 390/1500 | (4.16s) | train loss: 90.12, val loss: 134.71
[09:42:43] Epoch 400/1500 | (3.85s) | train loss: 87.67, val loss: 138.90
[09:43:22] Epoch 410/1500 | (3.51s) | train loss: 91.13, val loss: 93.63
[09:43:58] Epoch 420/1500 | (3.51s) | train loss: 88.04, val loss: 112.07
[09:44:34] Epoch 430/1500 | (3.55s) | train loss: 83.76, val loss: 112.57
[09:45:11] Epoch 440/1500 | (3.66s) | train loss: 86.35, val loss: 116.46
[09:45:51] Epoch 450/1500 | (3.63s) | train loss: 88.53, val loss: 101.72
[09:46:27] Epoch 460/1500 | (3.51s) | train loss: 85.50, val loss: 153.39
[09:47:15] Epoch 470/1500 | (4.61s) | train loss: 85.00, val loss: 120.23
[09:48:01] Epoch 480/1500 | (4.26s) | train loss: 81.28, val loss: 104.66
[09:48:42] Epoch 490/1500 | (3.82s) | train loss: 87.99, val loss: 123.68
[09:49:20] Epoch 500/1500 | (3.70s) | train loss: 82.95, val loss: 99.51
[09:50:01] Epoch 510/1500 | (3.98s) | train loss: 86.94, val loss: 108.87
[09:50:41] Epoch 520/1500 | (3.99s) | train loss: 91.10, val loss: 122.98
[09:51:23] Epoch 530/1500 | (4.54s) | train loss: 89.81, val loss: 108.39
[09:52:07] Epoch 540/1500 | (4.00s) | train loss: 85.41, val loss: 111.22
[09:52:49] Epoch 550/1500 | (3.99s) | train loss: 83.94, val loss: 104.77
[09:53:34] Epoch 560/1500 | (4.41s) | train loss: 80.88, val loss: 139.95
[09:54:18] Epoch 570/1500 | (4.22s) | train loss: 85.59, val loss: 119.91
[09:55:01] Epoch 580/1500 | (4.15s) | train loss: 90.69, val loss: 146.60
[09:55:44] Epoch 590/1500 | (4.12s) | train loss: 89.49, val loss: 136.70
[09:56:27] Epoch 600/1500 | (4.19s) | train loss: 82.59, val loss: 167.90
[09:57:09] Epoch 610/1500 | (4.07s) | train loss: 89.93, val loss: 138.59
[09:57:53] Epoch 620/1500 | (4.26s) | train loss: 96.15, val loss: 142.20
[09:58:37] Epoch 630/1500 | (4.20s) | train loss: 86.91, val loss: 106.33
[09:59:20] Epoch 640/1500 | (4.25s) | train loss: 90.46, val loss: 179.15
[10:00:02] Epoch 650/1500 | (4.46s) | train loss: 88.60, val loss: 137.37
[10:00:45] Epoch 660/1500 | (4.37s) | train loss: 84.77, val loss: 92.56
[10:01:28] Epoch 670/1500 | (4.26s) | train loss: 84.90, val loss: 102.42
[10:02:15] Epoch 680/1500 | (5.27s) | train loss: 88.33, val loss: 134.07
[10:02:58] Epoch 690/1500 | (4.18s) | train loss: 83.34, val loss: 157.23
[10:03:42] Epoch 700/1500 | (4.34s) | train loss: 78.55, val loss: 97.71
[10:04:26] Epoch 710/1500 | (4.22s) | train loss: 84.23, val loss: 190.50
[10:05:09] Epoch 720/1500 | (4.20s) | train loss: 78.45, val loss: 99.05
[10:05:53] Epoch 730/1500 | (4.11s) | train loss: 84.47, val loss: 144.31
[10:06:36] Epoch 740/1500 | (4.02s) | train loss: 84.71, val loss: 97.26
[10:07:19] Epoch 750/1500 | (4.01s) | train loss: 80.80, val loss: 94.72
[10:08:08] Epoch 760/1500 | (4.69s) | train loss: 84.83, val loss: 125.72
[10:08:53] Epoch 770/1500 | (4.00s) | train loss: 86.25, val loss: 127.83
[10:09:36] Epoch 780/1500 | (4.29s) | train loss: 79.94, val loss: 102.46
[10:10:19] Epoch 790/1500 | (4.18s) | train loss: 75.47, val loss: 90.93
[10:11:01] Epoch 800/1500 | (4.11s) | train loss: 75.50, val loss: 105.23
[10:11:41] Epoch 810/1500 | (4.07s) | train loss: 76.85, val loss: 117.17
[10:12:23] Epoch 820/1500 | (3.79s) | train loss: 77.68, val loss: 120.62
[10:13:00] Epoch 830/1500 | (3.64s) | train loss: 75.53, val loss: 117.50
[10:13:37] Epoch 840/1500 | (3.43s) | train loss: 78.20, val loss: 102.41
[10:14:13] Epoch 850/1500 | (3.58s) | train loss: 76.35, val loss: 249.63
[10:14:55] Epoch 860/1500 | (4.80s) | train loss: 73.30, val loss: 93.98
[10:15:37] Epoch 870/1500 | (3.63s) | train loss: 77.88, val loss: 110.33
[10:16:14] Epoch 880/1500 | (3.67s) | train loss: 73.00, val loss: 165.59
[10:16:51] Epoch 890/1500 | (3.52s) | train loss: 72.62, val loss: 90.09
[10:17:27] Epoch 900/1500 | (3.57s) | train loss: 72.56, val loss: 114.38
[10:18:04] Epoch 910/1500 | (3.45s) | train loss: 71.26, val loss: 93.73
[10:18:45] Epoch 920/1500 | (5.30s) | train loss: 73.88, val loss: 169.16
[10:19:22] Epoch 930/1500 | (3.49s) | train loss: 71.43, val loss: 157.88
[10:20:01] Epoch 940/1500 | (4.06s) | train loss: 69.15, val loss: 107.46
[10:20:39] Epoch 950/1500 | (3.48s) | train loss: 75.60, val loss: 107.58
[10:21:15] Epoch 960/1500 | (3.54s) | train loss: 78.14, val loss: 82.75
[10:21:52] Epoch 970/1500 | (3.53s) | train loss: 74.14, val loss: 119.17
[10:22:28] Epoch 980/1500 | (3.53s) | train loss: 69.60, val loss: 146.37
[10:23:05] Epoch 990/1500 | (3.93s) | train loss: 70.68, val loss: 79.31
[10:23:42] Epoch 1000/1500 | (3.70s) | train loss: 72.12, val loss: 93.38
[10:24:19] Epoch 1010/1500 | (3.64s) | train loss: 72.17, val loss: 97.39
[10:24:57] Epoch 1020/1500 | (3.73s) | train loss: 72.02, val loss: 113.19
[10:25:35] Epoch 1030/1500 | (3.68s) | train loss: 72.70, val loss: 160.87
[10:26:11] Epoch 1040/1500 | (3.52s) | train loss: 68.05, val loss: 77.50
[10:26:48] Epoch 1050/1500 | (3.58s) | train loss: 73.90, val loss: 129.97
[10:27:24] Epoch 1060/1500 | (3.46s) | train loss: 69.08, val loss: 122.59
[10:28:00] Epoch 1070/1500 | (3.67s) | train loss: 72.39, val loss: 160.51
[10:28:37] Epoch 1080/1500 | (3.53s) | train loss: 66.26, val loss: 155.73
[10:29:13] Epoch 1090/1500 | (3.45s) | train loss: 66.70, val loss: 80.56
[10:29:50] Epoch 1100/1500 | (3.67s) | train loss: 70.47, val loss: 104.98
[10:30:28] Epoch 1110/1500 | (3.57s) | train loss: 58.90, val loss: 172.86
[10:31:06] Epoch 1120/1500 | (3.61s) | train loss: 69.27, val loss: 120.87
[10:31:44] Epoch 1130/1500 | (3.76s) | train loss: 66.31, val loss: 80.33
[10:32:20] Epoch 1140/1500 | (3.41s) | train loss: 63.73, val loss: 95.57
[10:32:57] Epoch 1150/1500 | (3.80s) | train loss: 70.28, val loss: 92.49
[10:33:36] Epoch 1160/1500 | (3.54s) | train loss: 65.24, val loss: 90.94
[10:34:12] Epoch 1170/1500 | (3.49s) | train loss: 65.18, val loss: 80.06
[10:34:49] Epoch 1180/1500 | (3.62s) | train loss: 71.64, val loss: 72.58
[10:35:26] Epoch 1190/1500 | (3.62s) | train loss: 76.45, val loss: 57.84
[10:36:02] Epoch 1200/1500 | (3.63s) | train loss: 69.17, val loss: 95.70
[10:36:39] Epoch 1210/1500 | (3.90s) | train loss: 69.67, val loss: 138.75
[10:37:16] Epoch 1220/1500 | (3.45s) | train loss: 76.45, val loss: 141.73
[10:37:52] Epoch 1230/1500 | (3.72s) | train loss: 61.80, val loss: 82.10
[10:38:30] Epoch 1240/1500 | (3.63s) | train loss: 74.01, val loss: 103.25
[10:39:07] Epoch 1250/1500 | (3.54s) | train loss: 76.27, val loss: 98.37
[10:39:44] Epoch 1260/1500 | (3.69s) | train loss: 79.39, val loss: 124.40
[10:40:21] Epoch 1270/1500 | (3.79s) | train loss: 66.67, val loss: 101.26
[10:40:58] Epoch 1280/1500 | (3.49s) | train loss: 76.86, val loss: 106.25
[10:41:35] Epoch 1290/1500 | (3.76s) | train loss: 68.23, val loss: 118.69
[10:42:12] Epoch 1300/1500 | (3.59s) | train loss: 68.98, val loss: 83.94
[10:42:51] Epoch 1310/1500 | (3.54s) | train loss: 66.48, val loss: 107.75
[10:43:28] Epoch 1320/1500 | (3.80s) | train loss: 62.08, val loss: 73.10
[10:44:06] Epoch 1330/1500 | (3.64s) | train loss: 74.44, val loss: 88.70
[10:44:42] Epoch 1340/1500 | (3.59s) | train loss: 76.11, val loss: 147.46
[10:45:19] Epoch 1350/1500 | (3.55s) | train loss: 72.79, val loss: 76.91
[10:45:56] Epoch 1360/1500 | (4.01s) | train loss: 65.89, val loss: 86.49
[10:46:33] Epoch 1370/1500 | (3.96s) | train loss: 65.93, val loss: 126.73
[10:47:09] Epoch 1380/1500 | (3.51s) | train loss: 63.57, val loss: 90.77
[10:47:45] Epoch 1390/1500 | (3.55s) | train loss: 67.86, val loss: 121.91
[10:48:22] Epoch 1400/1500 | (3.60s) | train loss: 66.72, val loss: 107.05
[10:48:58] Epoch 1410/1500 | (3.53s) | train loss: 68.98, val loss: 106.44
[10:49:34] Epoch 1420/1500 | (3.58s) | train loss: 62.91, val loss: 69.03
[10:50:10] Epoch 1430/1500 | (3.54s) | train loss: 61.80, val loss: 75.59
[10:50:47] Epoch 1440/1500 | (3.52s) | train loss: 75.21, val loss: 72.03
[10:51:23] Epoch 1450/1500 | (3.53s) | train loss: 70.85, val loss: 83.35
[10:52:00] Epoch 1460/1500 | (3.55s) | train loss: 79.09, val loss: 108.59
[10:52:36] Epoch 1470/1500 | (3.47s) | train loss: 76.91, val loss: 85.50
[10:53:12] Epoch 1480/1500 | (3.54s) | train loss: 73.65, val loss: 76.41
[10:53:48] Epoch 1490/1500 | (3.54s) | train loss: 76.92, val loss: 131.97
[10:54:25] Epoch 1500/1500 | (3.48s) | train loss: 72.71, val loss: 98.09
`Trainer.fit` stopped: `max_epochs=1500` reached.
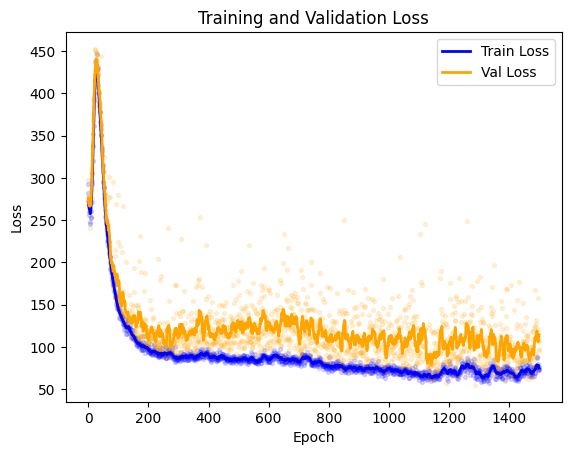
Check the loss#
Let’s examine the loss. We can access the fitting metrics using: model.metrics, which produces a pandas.DataFrame.
[7]:
model.metrics.head()
[7]:
| epoch | epoch_train_loss | epoch_validation_loss | opt_param_group_lr | sinkhorn_2.0_training | sinkhorn_2.0_validation | sinkhorn_4.0_training | sinkhorn_4.0_validation | sinkhorn_6.0_training | sinkhorn_6.0_validation | ... | velo_g_4.0_training | velo_g_4.0_validation | velo_g_6.0_training | velo_g_6.0_validation | velo_ratio_2.0_training | velo_ratio_2.0_validation | velo_ratio_4.0_training | velo_ratio_4.0_validation | velo_ratio_6.0_training | velo_ratio_6.0_validation | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | NaN | NaN | 0.0001 | 0.0 | NaN | 101.126320 | NaN | 196.767059 | NaN | ... | 1.350286 | NaN | 1.371000 | NaN | 621.440247 | NaN | 621.460449 | NaN | 621.499084 | NaN |
| 1 | 0 | NaN | NaN | 0.0001 | 0.0 | NaN | 98.033127 | NaN | 192.716980 | NaN | ... | 1.266959 | NaN | 1.274758 | NaN | 618.020935 | NaN | 618.065552 | NaN | 618.118164 | NaN |
| 2 | 0 | NaN | NaN | 0.0001 | 0.0 | NaN | 102.906174 | NaN | 186.784790 | NaN | ... | 1.207190 | NaN | 1.205150 | NaN | 614.259155 | NaN | 614.308716 | NaN | 614.347595 | NaN |
| 3 | 0 | NaN | 268.880798 | 0.0001 | NaN | 0.0 | NaN | 81.281403 | NaN | 187.599396 | ... | NaN | 1.044867 | NaN | 1.036563 | NaN | 609.063049 | NaN | 609.094971 | NaN | 609.27179 |
| 4 | 0 | 292.778168 | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | ... | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN | NaN |
5 rows × 30 columns
[10]:
import matplotlib.pyplot as plt
train_loss = model.metrics[['epoch', 'epoch_train_loss']].dropna().reset_index(drop=True)
val_loss = model.metrics[['epoch', 'epoch_validation_loss']].dropna().reset_index(drop=True)
# Plot raw values as scatter points
plt.scatter(train_loss['epoch'], train_loss['epoch_train_loss'], color='blue', s=8, alpha=0.15)
plt.scatter(val_loss['epoch'], val_loss['epoch_validation_loss'], color='orange', s=8, alpha=0.15)
# Compute moving averages
train_loss_ma = train_loss['epoch_train_loss'].rolling(window=10, min_periods=1, center=True).mean()
val_loss_ma = val_loss['epoch_validation_loss'].rolling(window=10, min_periods=1, center=True).mean()
# Plot moving averages as lines
plt.plot(train_loss['epoch'], train_loss_ma, color='blue', linewidth=2, label='Train Loss')
plt.plot(val_loss['epoch'], val_loss_ma, color='orange', linewidth=2, label='Val Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training and Validation Loss')
plt.legend()
plt.show()
Project the learned dynamics onto the original input data#
[11]:
model.drift()
scDiffEq [INFO]: Added: adata.obsm['X_drift']
scDiffEq [INFO]: Added: adata.obsm['drift']
[12]:
model.diffusion()
scDiffEq [INFO]: Added: adata.obsm['X_diffusion']
scDiffEq [INFO]: Added: adata.obsm['diffusion']
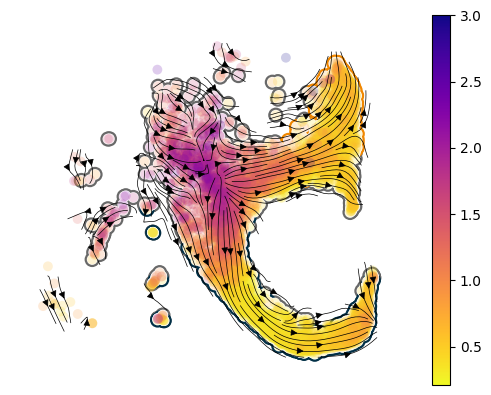
Make a stream plot#
Let’s take a qualitative peek at the learned velocity. Here, we plot the learned drift function (the 2x512 fully-connected network) as the the vectory field. While we sample the diffusion field and plot the magnitude of diffusion and denote this using the colormap.
First, we need to make the velocity graph - this is mostly borrowed from the scvelo implementation.
[13]:
sdq.tl.velocity_graph(model.adata)
scDiffEq [INFO]: Added: adata.obsp['distances']
scDiffEq [INFO]: Added: adata.obsp['connectivities']
scDiffEq [INFO]: Added: adata.uns['neighbors']
scDiffEq [INFO]: Added: adata.obsp['velocity_graph']
scDiffEq [INFO]: Added: adata.obsp['velocity_graph_neg']
[16]:
import cellplots
cmap = {
"Undifferentiated": "dimgrey", #"#f0efeb",
"Neutrophil": "#023047",
"Monocyte": "#F08700",
}
axes = cellplots.umap_manifold(model.adata, groupby="Cell type annotation", c_background=cmap)
sdq.pl.velocity_stream(model.adata, c = "diffusion", ax=axes[0], scatter_kwargs={"vmax": 3})
Sample and visualize trajectories#
We can generatively simulate trajectories from the original dataset and study them furhter to take on a granular view of the developmental dynamics. Here, we’ll use dt=0.1d. The LARRY dataset provides measurements at multiple time points, allowing us to interpolate and extrapolate developmental trajectories with high temporal resolution.
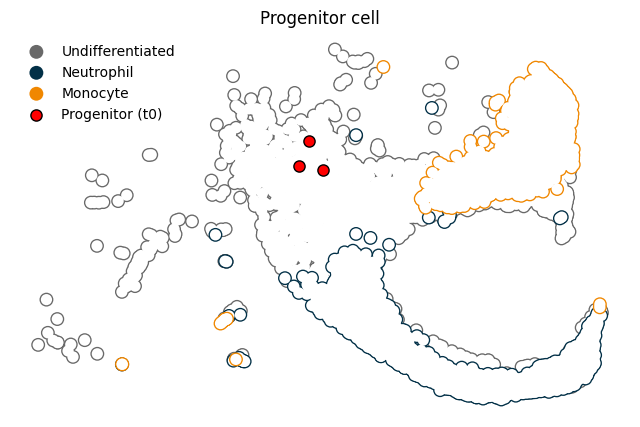
Isolate some early progenitor cells and sample a few to start from#
[17]:
progenitor = (
model.adata.obs.loc[model.adata.obs["Time point"] == model.adata.obs["Time point"].min()]
.loc[model.adata.obs["Cell type annotation"] == "Undifferentiated"]
.sample(3)
)
progenitor
[17]:
| Library | Cell barcode | Time point | Starting population | Cell type annotation | Well | SPRING-x | SPRING-y | clone_idx | fate_observed | ... | ct_score | ct_pseudotime | ct_num_exp_genes | nm_clones | W | test | fit_train | fit_val | drift | diffusion | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2390 | d2_2 | TGCTTGGG-GGTCCCTT | 2.0 | Lin-Kit+Sca1- | Undifferentiated | 0 | 256.944 | 424.535 | 3801.0 | True | ... | 0.0474299712113319 | 0.952570 | 236 | True | 1 | False | True | False | 26.022032 | 1.925547 |
| 2334 | d2_3 | AATAAGGA-GAAGCACT | 2.0 | Lin-Kit+Sca1- | Undifferentiated | 0 | 303.865 | 313.636 | 2693.0 | True | ... | 0.068739448002275 | 0.931261 | 320 | True | 1 | False | True | True | 37.883366 | 1.771815 |
| 4974 | LSK_d2_1 | GTCTTCCT-GCGCATTC | 2.0 | Lin-Kit+Sca1+ | Undifferentiated | 0 | 470.467 | 464.074 | 3560.0 | True | ... | 0.0636405458432328 | 0.936359 | 179 | True | 1 | False | False | False | 31.065161 | 1.441383 |
3 rows × 22 columns
[18]:
grouped = model.adata.obs.groupby("Cell type annotation")
x0 = model.adata[progenitor.index].obsm["X_umap"].toarray()
fig, ax = plt.subplots(1, 1, figsize=(8, 5))
for group in ["Undifferentiated", "Neutrophil", "Monocyte"]:
group_ix = grouped.get_group(group).index
xu = model.adata[group_ix].obsm["X_umap"]
ax.scatter(xu[:, 0], xu[:, 1], c=cmap[group], label=group, ec = "None", rasterized=True, s = 100)
ax.scatter(xu[:, 0], xu[:, 1], c="white", ec = "None", rasterized=True, s = 65)
ax.scatter(x0[:, 0], x0[:, 1], c="r", s=65, ec="k", label = "Progenitor (t0)")
ax.legend(facecolor="None", edgecolor="None")
ax.set_title("Progenitor cell")
ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)
ax.spines[['top', 'right', 'bottom', 'left']].set_visible(False)
[19]:
adata_sim = sdq.tl.simulate(
adata, idx=progenitor.index, N=512, diffeq=model.DiffEq, time_key="Time point"
)
print(adata_sim)
AnnData object with n_obs × n_vars = 62976 × 50
obs: 't', 'z0_idx', 'sim_i', 'sim'
uns: 'sim_idx', 'simulated'
[20]:
sdq.tl.annotate_cell_state(adata_sim, kNN=model.kNN, obs_key="Cell type annotation")
scDiffEq [INFO]: Bulding Annoy kNN Graph on adata.obsm['train']
scDiffEq [INFO]: Added state annotation: adata_sim.obs['Cell type annotation']
[21]:
sdq.tl.annotate_cell_fate(adata_sim, state_key="Cell type annotation")
scDiffEq [INFO]: Added fate annotation: adata_sim.obs['fate']
scDiffEq [INFO]: Added fate counts: adata_sim.uns['fate_counts']
[22]:
adata_sim.uns["fate_counts"]
[22]:
{'Neutrophil': 1080, 'Monocyte': 318, 'Undifferentiated': 138}
Fit UMAP model to the training data
We can use adata_sim.X because our predictions (which are stored in .X) were made in the PCA space.
[23]:
adata_sim.obsm["X_umap"] = UMAP.transform(adata_sim.X)
[24]:
def plot_background(adata, ax):
grouped = adata.obs.groupby("Cell type annotation")
for group in ["Undifferentiated", "Neutrophil", "Monocyte"]:
group_ix = grouped.get_group(group).index
xu = model.adata[group_ix].obsm["X_umap"]
ax.scatter(xu[:, 0], xu[:, 1], c=cmap[group], label=group, ec = "None", rasterized=True, s = 100)
ax.scatter(xu[:, 0], xu[:, 1], c="white", ec = "None", rasterized=True, s = 65)
ax.scatter(x0[:, 0], x0[:, 1], c="r", s=65, ec="k", label = "Progenitor (t0)")
ax.legend(facecolor="None", edgecolor="None")
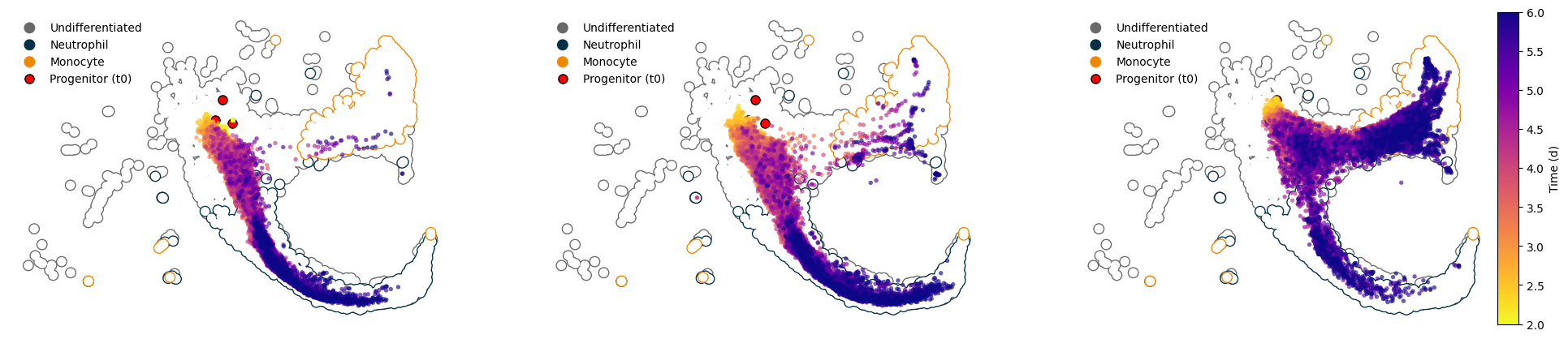
[25]:
fig, axes = plt.subplots(1, 3, figsize=(24, 5))
for en, (progenitor, group_df) in enumerate(adata_sim.obs.groupby("z0_idx")):
ax = axes[en]
ax.tick_params(left=False, bottom=False, labelleft=False, labelbottom=False)
ax.spines[['top', 'right', 'bottom', 'left']].set_visible(False)
plot_background(adata, ax)
fate_subset = adata_sim[group_df.index]
img = cellplots.umap(fate_subset, ax=ax, c=fate_subset.obs["t"], s=15, alpha=0.65, ec="None", cmap="plasma_r")
import numpy as np
import matplotlib.colors
from mpl_toolkits.axes_grid1 import make_axes_locatable
divider = make_axes_locatable(axes[-1])
cax = divider.append_axes("right", size="5%", pad=0.05)
sm = plt.cm.ScalarMappable(norm=matplotlib.colors.Normalize(vmin=np.min(adata_sim.obs["t"]), vmax=np.max(adata_sim.obs["t"])), cmap="plasma_r")
sm.set_array([])
plt.colorbar(sm, cax=cax, label="Time (d)")
[25]:
<matplotlib.colorbar.Colorbar at 0x14a78a110>
Gene-level analyses#
[ ]:
scaler_model = sdq.io.read_pickle("/Users/mvinyard/data/scdiffeq_data/larry/scaler.pkl")
PCA = sdq.io.read_pickle("/Users/mvinyard/data/scdiffeq_data/larry/pca.pkl")
[ ]:
sdq.tl.annotate_gene_features(adata_sim, adata, PCA=PCA, gene_id_key="gene_ids")
sdq.tl.invert_scaled_gex(adata_sim, scaler_model = scaler_model)
scDiffEq [INFO]: Gene names added to: `adata_sim.uns['gene_ids']`
scDiffEq [INFO]: Inverted expression added to: `adata_sim.obsm['X_gene']`
[ ]:
adata_sim.uns['sim_idx'] = list(adata_sim.uns['sim_idx'])
adata_sim.uns["gene_ids"] = adata_sim.uns["gene_ids"].to_dict()
adata_sim.write_h5ad("./adata_sim.larry.h5ad")
print(adata_sim)
AnnData object with n_obs × n_vars = 62976 × 50
obs: 't', 'z0_idx', 'sim_i', 'sim', 'Cell type annotation', 'fate'
uns: 'sim_idx', 'simulated', 'fate_counts', 'gene_ids'
obsm: 'X_umap', 'X_gene', 'X_gene_inv'
[ ]:
import pandas as pd
def mean_and_std_expr(df, adata_sim, gene):
x = adata_sim[df.index].obsm["X_gene_inv"][gene]
return pd.Series({'mean': x.mean(), 'std': x.std()})
[ ]:
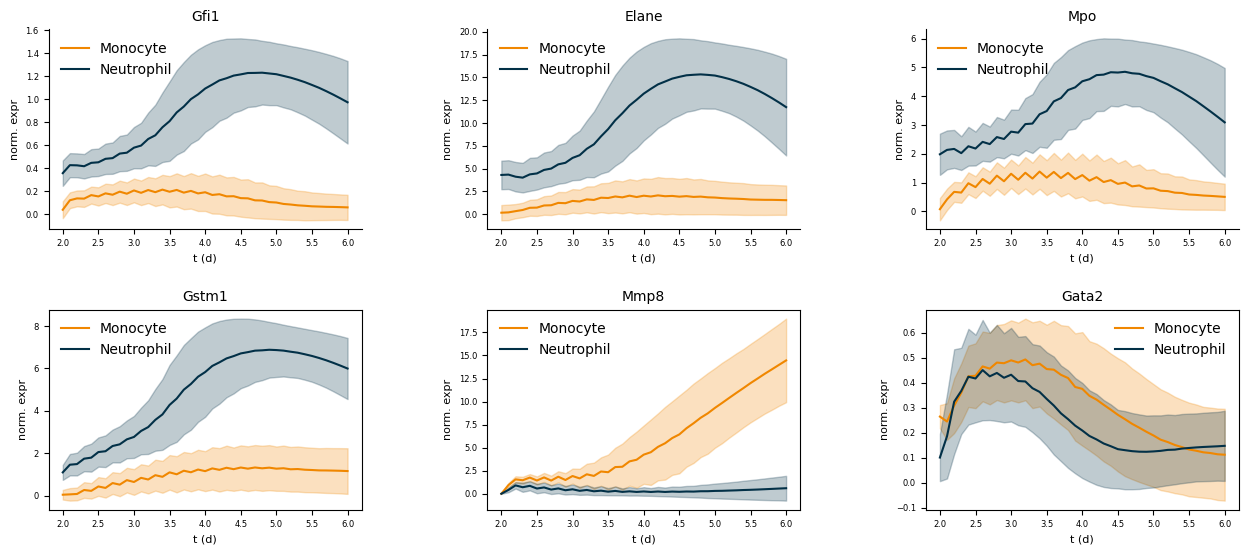
genes = ["Gfi1", "Elane", "Mpo", "Gstm1", "Mmp8", "Gata2"]
means = []
stds = []
for gene in genes:
res = adata_sim.obs.groupby(["t", "fate"]).apply(mean_and_std_expr, adata_sim=adata_sim, gene=gene)
mean_df = res['mean'].unstack()
std_df = res['std'].unstack()
means.append(mean_df)
stds.append(std_df)
[ ]:
fig, axes = cellplots.plot(
6,
3,
height=0.65,
width=0.8,
wspace=0.4,
hspace=0.4,
x_label=["t (d)"],
y_label=["norm. expr"],
title=genes,
delete=[["top", "right"]] * 3,
)
for en, (mean_df, std_df) in enumerate(zip(means, stds)):
for col in mean_df:
if col != "Undifferentiated":
color = cmap[col]
# Plot mean with line
axes[en].plot(mean_df.index, mean_df[col], label=col, c=color)
lower = mean_df[col] - std_df[col]
upper = mean_df[col] + std_df[col]
axes[en].fill_between(
mean_df.index,
lower,
upper,
color=color,
alpha=0.25
)
axes[en].legend(facecolor="None", edgecolor="None")