Figure S5

Import packages

import scdiffeq as sdq
import dev
import cellplots as cp
import matplotlib.pyplot as plt
import matplotlib.cm as cm
import pandas as pd
import numpy as np

Read data and load project

h5ad_path = (
    "/home/mvinyard/data/adata.reprocessed_19OCT2023.more_feature_inclusive.h5ad"
)
adata = sdq.io.read_h5ad(h5ad_path)

AnnData object with n_obs × n_vars = 130887 × 2492
    obs: 'Library', 'Cell barcode', 'Time point', 'Starting population', 'Cell type annotation', 'Well', 'SPRING-x', 'SPRING-y', 'clone_idx', 'fate_observed', 't0_fated', 'train'
    var: 'gene_ids', 'hv_gene', 'must_include', 'exclude', 'use_genes'
    uns: 'fate_counts', 'h5ad_path', 'time_occupance'
    obsm: 'X_clone', 'X_pca', 'X_umap', 'cell_fate_df'
    layers: 'X_scaled'

project = sdq.io.Project(path="./LightningSDE-FixedPotential-RegularizedVelocityRatio/")

Compute fate prediction accuracy for each version

RATIOS = {}
for version, path in project._VERSION_PATHS.items():
    try:
        v = getattr(project, version)
        acc = dev.fate_prediction_accuracy(v)
        target_ratio = v.hparams["velocity_ratio_params"]["target"]
        RATIOS[version] = target_ratio, v, acc
    except:
        pass

For each un-regularized training run, compute drift [f] and diffusion [g]

def f(df, key="training"):
    return df.filter(regex="velo_f").filter(regex=key).dropna().sum(1).mean()


def g(df, key="training"):
    return df.filter(regex="velo_g").filter(regex=key).dropna().sum(1).mean()


UnEnforcedResults = {}
for en, (version, results) in enumerate(RATIOS.items()):
    target_ratio, v, acc = results
    if v.hparams["velocity_ratio_params"]["enforce"] == 0:
        print(version)
        grouped = v.metrics_df.groupby("epoch")
        UnEnforcedResults[version] = {
            "f_training": grouped.apply(f, key="training"),
            "f_validation": grouped.apply(f, key="validation"),
            "g_training": grouped.apply(g, key="training"),
            "g_validation": grouped.apply(g, key="validation"),
        }

version_0
version_1
version_2
version_3
version_4

Plot un-regularized drift and diffusion

colors = ["#33658a", "#86bbd8", "#758e4f", "#f6ae2d", "#f26419"]

seeds = {
    "version_0": 0,
    "version_1": 1,
    "version_2": 2,
    "version_3": 3,
    "version_4": 4,
}

fig, axes = cp.plot(
    2,
    2,
    wspace=0.2,
    height=0.6,
    width=0.6,
    title=["Unregularized [f/g]: training", "f/g: validation"],
    x_label=["Epoch", "Epoch"],
    y_label=["f/g", "f/g"],
)
for i, (k, v) in enumerate(UnEnforcedResults.items()):
    r_training = v["f_training"].div(v["g_training"])
    r_validation = v["f_validation"].div(v["g_validation"])

    for en, r_df in enumerate([r_training, r_validation]):
        x, y = r_df.index, r_df.values
        xy = r_df.rolling(window=50).mean().dropna()
        c = colors[i]
        axes[en].scatter(
            x, y, c=c, alpha=0.1, s=5, ec="None", zorder=1, rasterized=True
        )
        axes[en].plot(xy, c=c, lw=1, label=seeds[k], zorder=2, rasterized=True)


for ax in axes:
    ax.set_ylim(0, 1.2)
    ax.legend(edgecolor="None", facecolor="None")
    ax.grid(True, c="lightgrey", lw=0.5, zorder=0)
    ax.xaxis.set_tick_params(width=0.5)
    ax.yaxis.set_tick_params(width=0.5)

plt.savefig(
    "unenforced_drift_diffusion_ration.training_validation.suppl_fig_s5.svg", dpi=500
)

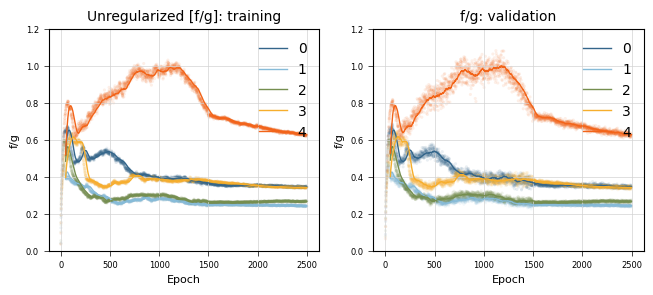
Compute the empirical unregularized ratio of f and g

unenforced_ratio = np.array(
    [
        v["f_validation"].iloc[-1] / v["g_validation"].iloc[-1]
        for i, (k, v) in enumerate(UnEnforcedResults.items())
    ]
)
unenforced_ratio.mean(), unenforced_ratio.std()

(0.3669882612570243, 0.13488926187436895)

rel = unenforced_ratio / (1 + unenforced_ratio)
print(rel.mean(), rel.std())
print(unenforced_ratio.mean() / (1 + unenforced_ratio.mean()))

0.26198354528285633 0.06584885182554004
0.2684648227480443